Basic matrix maths for neural networks: in practice
This is the second post in my short series of tutorials on matrix operations for neural networks, targeted at beginners, and at people who have some practical experience, but who haven't yet dug into the underlying theory. Again, if you're an experienced ML practitioner, you should skip this post -- though if you want to read it anyway, any comments or suggestions for improvements would be much appreciated!
In my last post in the series, I showed how to derive the formulae to run a neural network from the basic principles of matrix maths. I gave two formulae that are generally used in mathematical treatments of NNs -- one with a separate bias matrix:
...and one with the bias terms baked into the weights matrix, and the inputs matrix extended with a row of s at the bottom:
However, I finished off by saying that in real production implementations, people normally use this instead:
...which you might have seen in production PyTorch code looking like this:
Z = X @ W.T + B
This post explores why that form of the equation works better in practice.
Basic matrix maths for neural networks: the theory
I thought it would be worth writing a post on how matrix multiplication is used to calculate the output of neural networks. We use matrices because they make the maths easier, and because GPUs can work with them efficiently, allowing us to do a whole bunch of calculations with a single step -- so it's really worth having a solid grounding in what the underlying operations are.
If you're an experienced ML practitioner, you should skip this post. But you might find it useful if you're a beginner -- or if, like me until I started working through this, you've coded neural networks and used matrix operations for them, but apart from working through an example or two by hand, you've never thought through the details.
In terms of maths, I'll assume that you know what a vector is, what a matrix is, and have some vague memories of matrix multiplication from your schooldays, but that's it -- everything else I will define.
In terms of neural networks, I'll assume that you are aware of their basic layout and how they work in a general sense -- but there will be diagrams for clarity and I'll define specific terms.
So, with expectations set, let's go!
Getting MathML to render properly in Chrome, Chromium and Brave
The other day I posted about adding mathematical typesetting to this blog using markdown2, LaTeX and MathML. One problem that remained at the end of that was that it looked a bit rubbish; in particular, the brackets surrounding matrices were just one line high, albeit centred, like this:
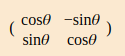
...rather than stretched to the height of the matrix, like this example from KaTex:
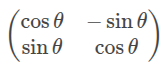
After posting that, I discovered that the problem only existed in Chromium-based browsers. I saw it in Chromium, Chrome and Brave on Android and Linux, but in Firefox on Linux, and on Safari on an iPhone, it rendered perfectly well.
Guided by the answers to this inexplicably-quiet Stack Overflow question,
I discovered that the prolem is the math fonts available on Chromium-based browsers.
Mathematical notation, understandably, needs specialised fonts. Firefox and Safari
either have these pre-installed, or do something clever to adapt the fonts you
are using (I suspect the former, but Firefox developer tools told me that it was
using my default body text font for <math> elements). Chromium-based browsers
do not, so you need to provide one in your CSS.
Using Frédéric Wang's MathML font test page,
I decided I wanted to use the STIX font. It was a bit tricky to find a downloadable
OTF file (you specifically need the "math" variant of the font -- in the same way
as you might find -italic and -bold files to download, you can find -math
ones) but I eventually found a link on this MDN page.
I put the .otf file in my font assets directory, then added the appropriate stuff
to my CSS -- a font face definition:
@font-face {
font-family: 'STIX-Two-Math';
src: url('/fonts/STIXTwoMath-Regular.otf') format('opentype');
}
...and a clause saying it should be used for <math> tags:
math {
font-family: STIX-Two-Math;
font-size: larger;
}
The larger font size is because by default it was rendering about one third of
the height of my body text -- not completely happy about that, as it feels like an
ad-hoc hack, but it will do for now.
Anyway, mathemetical stuff now renders pretty well! Here's the matrix from above, using my new styling:
I hope that's useful for anyone else hitting the same problem.
[Update: because RSS readers don't load the CSS, the bad rendering still shows up in NewsBlur's Android app, which I imagine must be using Chrome under the hood for its rendering. Other RSS readers are probably the same :-(]
Adding mathematical typesetting to the blog
I've spent a little time over the weekend adding the ability to post stuff in mathematical notation on this blog. For example:
It should render OK in any browser released after early 2023; I suspect that many RSS readers won't be able to handle it right now, but that will hopefully change over time. [Update: my own favourite, NewsBlur, handles it perfectly!]
Here's why I wanted to do that, and how I did it.
Writing an LLM from scratch, part 7 -- wrapping up non-trainable self-attention
This is the seventh post in my series of notes on Sebastian Raschka's book "Build a Large Language Model (from Scratch)". Each time I read part of it, I'm posting about what I found interesting or needed to think hard about, as a way to help get things straight in my own head -- and perhaps to help anyone else that is working through it too.
This post is a quick one, covering just section 3.3.2, "Computing attention weights for all input tokens". I'm covering it in a post on its own because it gets things in place for what feels like the hardest part to grasp at an intuitive level -- how we actually design a system that can learn how to generate attention weights, which is the subject of the next section, 3.4. My linear algebra is super-rusty, and while going through this one, I needed to relearn some stuff that I think I must have forgotten sometime late last century...
Writing an LLM from scratch, part 6 -- starting to code self-attention
This is the sixth in my series of notes on Sebastian Raschka's book "Build a Large Language Model (from Scratch)". Each time I read part of it, I'm posting about what I found interesting as a way to help get things straight in my own head -- and perhaps to help anyone else that is working through it too. This post covers just one subsection of the trickiest chapter in the book -- subsection 3.3.1, "A simple self-attention mechanism without trainable weights". I feel that there's enough in there to make up a post on its own. For me, it certainly gave me one key intuition that I think is a critical part of how everything fits together.
As always, there may be errors in my understanding below -- I've cross-checked and run the whole post through Claude, ChatGPT o1, and DeepSeek r1, so I'm reasonably confident, but caveat lector :-) With all that said, let's go!
Writing an LLM from scratch, part 5 -- more on self-attention
I'm reading Sebastian Raschka's book "Build a Large Language Model (from Scratch)", and posting about what I found interesting every day that I read some of it. In retrospect, it was kind of adorable that I thought I could get it all done over my Christmas break, given that I managed just the first two-and-a-half chapters! However, now that the start-of-year stuff is out of the way at work, hopefully I can continue. And at least the two-week break since my last post in this series has given things some time to stew.
In the last post I was reading about attention mechanisms and how they work, and was a little thrown by the move from attention to self-attention, and in this blog post I hope to get that all fully sorted so that I can move on to the rest of chapter 3, and then the rest of the book. Rashka himself said on X that this chapter "might be the most technical one (like building the engine of a car) but it gets easier from here!" That's reassuring, and hopefully it means that my blog posts will speed up too once I'm done with it.
But first: on to attention and what it means in the LLM sense.
Writing an LLM from scratch, part 4
I'm reading Sebastian Raschka's book "Build a Large Language Model (from Scratch)", and posting about what I found interesting every day that I read some of it.
Here's a link to the previous post in this series.
Today I read through chapter 3, which introduces and explains attention mechanisms -- the core architecture that allows LLMs to "understand" the meaning of text in terms of the relationships between words. This feels like the core of the book; at least, for me, it's the part of the underlying workings of LLMs that I understand the least. I knew it was something to do with the LLM learning which other words to pay attention to when looking at a particular one, but that's pretty much it.
And it's a tough chapter. I finished with what I felt was a good understanding at a high level of how the calculations that make up self-attention in an LLM work -- but not of how self-attention itself works. That is, I understood how to write one, in terms of the steps to follow mathematically, but not why that specific code would be what I would write or why we would perform those mathematical operations.
I think this was because I tried to devour it all in a day, so I'm going to go through much more slowly, writing up notes on each section each day.
Today, I think, I can at least cover the historical explanation of how attention mechanisms came to be in the first place, because that seems reasonably easy to understand.
Writing an LLM from scratch, part 3
I'm reading Sebastian Raschka's book "Build a Large Language Model (from Scratch)", and posting about what I found interesting every day that I read some of it.
Here's a link to the previous post in this series.
Today I was working through the second half of Chapter 2, "Working with text data", which I'd started just before Christmas. Only two days off, so it was reasonably fresh in my mind :-)
Writing an LLM from scratch, part 2
I'm reading Sebastian Raschka's book "Build a Large Language Model (from Scratch)", and planning to post every day (or at least, every day I read some of it -- Christmas day I suspect I'll not be posting) with notes on what I found interesting.
Here's a link to the previous post in this series.
I had been planning to do a chapter a day, but that is looking optimistic for such a dense book! So today, I've read the first half or so of Chapter 2, "Working with text data". This gives an overview of the pre-processing that happens to text before it hits the LLM, goes on to describe a simple tokenization system (complete with source code), and then briefly covers the byte pair encoding method that we'll actually be using for the LLM.