Messing around with fine-tuning LLMs, part 9 -- gradient checkpointing

Posted on 3 September 2024 in Programming, Python, AI

This is the 9th installment in my ongoing investigations into fine-tuning LLM models. My goal is to fine-tune an 8B model -- specifically, the Llama 3 8B base model -- on the openassistant-guanaco dataset, without using tricks like quantization or LoRA. I'm doing this as a way to try to understand how to do full-on multi-GPU training of a model that cannot be trained on just one GPU -- so I'm taking it super-slowly and stopping and measuring everything along the way, which means that I'm learning a ton of new stuff pretty effectively.

So far, I've:

I'll look into Liger in more depth in a future post, because it looks incredibly useful, but first I wanted to investigate something that I learned about as a result of my original post about it. I posted my results on X, and Byron Hsu (who's building Liger at LinkedIn) thought it was weird that I was only able to squeeze a batch size of two (without Liger) or three (with it) into an 8x A100 80 GiB machine. In the Liger GitHub repo, they have an example of the kind of memory improvements the new kernels can provide; it shows without-Liger memory usages of (roughly) 55 GiB at a batch size of 32, 67 GiB at 48, and an OOM with 64. Now, they're using a sequence length of 512 rather than the 2048 I've been using, and that would have an effect, but not enough to allow batches that were sixteen times larger -- expecially because their benchmarks were being run on a machine with four A100 80 GiB cards, not eight.

Byron and I had a quick chat just to see if there was anything obviously dumb going on in my configuration, and one thing that stood out to him was that I wasn't using gradient checkpointing (which the Liger example is doing). That was something I'd very briefly looked into back in my earliest experiments into tuning the 8B model; I was following a Hugging Face guide to what to do if you hit memory problems. In their guide to DeepSpeed, they write:

A general process you can use is (start with batch size of 1):

  1. enable gradient checkpointing
  2. try ZeRO-2
  3. try ZeRO-2 and offload the optimizer

I had tried running my tune with both the gradient checkpointing enabled and Zero-2, but it blew up at iteration 24 (my first indication that there was something that kicked in at that point that increased memory usage), so I'd moved straight on to the optimizer offload.

At that point I was using instances with 8x A100 40 GiB. Since then, I'd switched to using 80 GiB per GPU machines, and done various tests comparing performance:

But what would happen if I just tried Zero 3 with no optimizer offload, with and without gradient checkpointing? That really sounded worth a look.

So, while I finished off my last post by saying

I think I'm finally in a place where I can do what should be the last experiment in this series: a full fine-tune of the Llama 3 8B base model -- on the openassistant-guanaco dataset, without using tricks like quantization or LoRA.

...it now looks like there's something well worth investigating first: gradient checkpointing.

What is gradient checkpointing?

Obviously, the first thing to do was to work out what it actually was; I could just blindly call the functions to enable it, but the purpose of all of these experiments is to learn stuff, so let's learn.

The idea behind gradient checkpointing is to trade processing speed for memory usage; that is, to use less VRAM at the cost of more GPU (and thus slower training speed at a given batch size). Saving the VRAM is useful because those savings can be large enough that you can increase the batch size (perhaps dramatically), and by training with larger batches, although you might take longer for each batch, you might finish the overall train faster.

Some numbers might help to clarify that; let's say that you can fit a batch size of one into your VRAM. You are training over 1,000 examples, and taking one second per example. That takes 1,000 seconds in total.

Now you introduce gradient checkpointing. It increases the time for each batch -- let's say that it takes 1.3 seconds per iteration. Training with an unchanged batch size of one will now take 1,300 seconds.

However, in this case we'll imagine that it also frees up enough memory for you to increase the batch size to two. So now, your train will only have 500 iterations instead of 1,000, so you'll be able to train in 1.3 * 500 = 650 seconds, which is a big win! Of course, that's not quite realistic, as the seconds per iteration will go up with the increased batch size (in my last post I saw a linear relationship), but this increase will hopefully be less than a factor of two.

So, outside of degenerate cases (say, where you can train with a batch size of one without checkpointing, but adding on the checkpointing doesn't save enough VRAM to bump the batch size up to two), gradient checkpointing should be a net speedup.

(I had a long conversation with Claude about this, and it also suggested that the increased batch size can be useful beyond the performance boost; apparently, larger batch sizes can lead to better, more generalised training. Intuitively this makes sense. For an LLM, you can imagine that training it on the sentence "I like bacon", and then "I like cheese", and then "I like eggs", adjusting the weights after each one, might lead it to "learn" more from the first example than from the second, and more from the second than the third. Training on a batch of all three of them in one go and then doing a single adjustment of the weights afterwards seems like it might consider them all more equally. I'm doing a lot of hand-waving there, but hopefully what I'm trying to say comes through :-)

So that's why we might want to use it. How does this trade-off work in practice?

When we're training a multi-layer neural net, we do a forward pass -- where we put a batch of data through the network -- and get an output. We use the error function to work out how far off what we want that output was. We want to reduce the error, so we work out the partial derivative of that error against all of the parameters so that we have a gradient, and then we adjust each weight a small distance in the opposite direction to that gradient (because the gradient points "uphill" and we want to go downhill, in the direction of a lower error).

The tricky bit there is, of course, working out that derivative. And one of the inputs to the calculations that do that is the activations from that forward pass. It needs to know, for each neuron, what activations came in, and what came out.

So, when we're doing the forward pass, we normally store all of the activations, and keep them around so that when it's time to do the backward one, they're there waiting for us.

The problem is that they use up lots of VRAM. Imagine an 8B model, and that we're using 16-bit activations. That means that a forward pass through the model will mean that we need to store 2 bytes times 8 billion activations -- and that's with a batch size of one, because this will scale linearly with the number of inputs we're running through the network. So that's 16 GiB of activations with a batch size of 1, 32 GiB with a batch size of two, 48 GiB with three, and so on. That's rather a lot of memory, even if it's split between the different GPUs in a multi-GPU setup.

(As an aside, I believe this is one of the reasons why training is so much more hardware-intensive that inference. If you are just running an LLM and want to feed in an input and get the output, the only activations you need as you process each layer are the ones from the previous layer. Once you've done layer n, you can throw away the activations for layer n-1.)

What gradient checkpointing does is, essentially, only store some of the activations. LLMs are very deep networks -- that is, they have a large number of layers. So you just store the activations (a checkpoint) at specific layers -- exactly which will depend on the details of the model and how much VRAM savings you want. In the backward pass, you will still need all of the activations, but you can use the stored checkpointed ones to reconstruct them. This is relatively expensive in terms of processor time, but (as the examples above suggest) is still worthwhile because of the savings in memory usage.

So, that was the theory. What happened in practice?

Training the 0.5B model

As always, I started off with the 0.5B model that I can train locally. I used exactly the same code as I did for the no-optimizer-offload case last time around, apart from adding

model.gradient_checkpointing_enable()

...just after creating the model. I also decided to run this test both with and without expandable segments, as although my previous tests had shown that using that new memory management technique was invariably a win, this was a change in memory usage that I hadn't tried before in enough depth that I was sure that that would still apply.

Here's a plot of the results without expandable segments:

Memory usage and seconds/iteration vs batch size, 0.5B model, with gradient checkpointing, no expandable segments

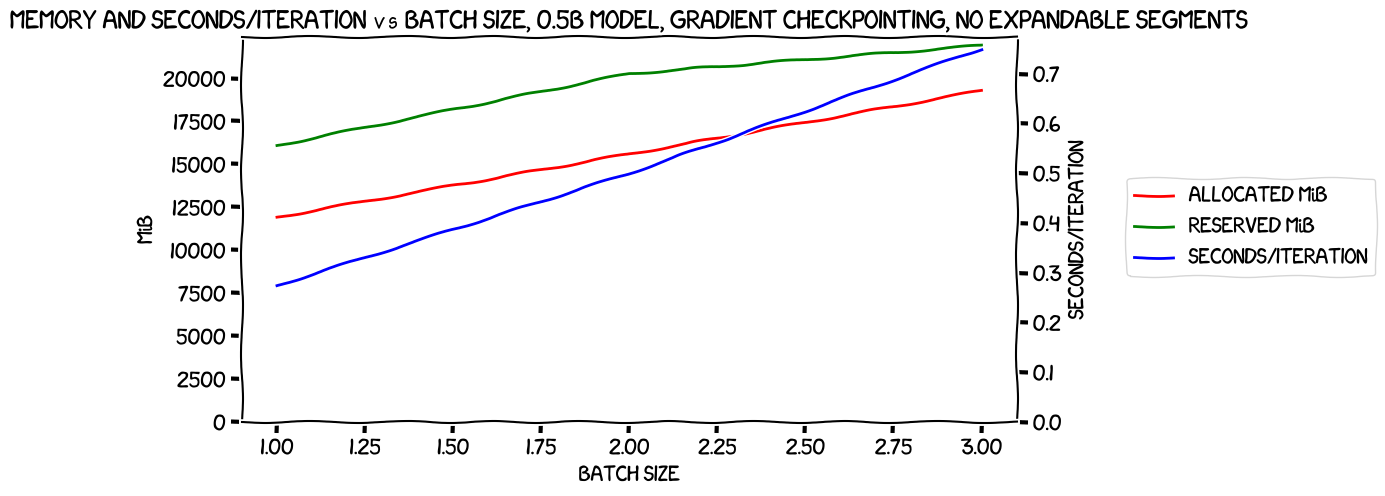
Pretty much what we normally see with these charts; memory uage (both allocated and reserved) are climbing pretty much linearly with the batch size, and so is seconds/iteration.

But what might not stand out (but did to me when I first saw the results, and will be clearer in a few charts' time) is that we got up to a batch size of three here, versus a maximum batch size of two without gradient checkpointing. So this change has definitely improved memory usage, as we'll see in a minute.

But first, let's check out what happened with expandable segments:

Memory usage and seconds/iteration vs batch size, 0.5B model, with gradient checkpointing, with expandable segments

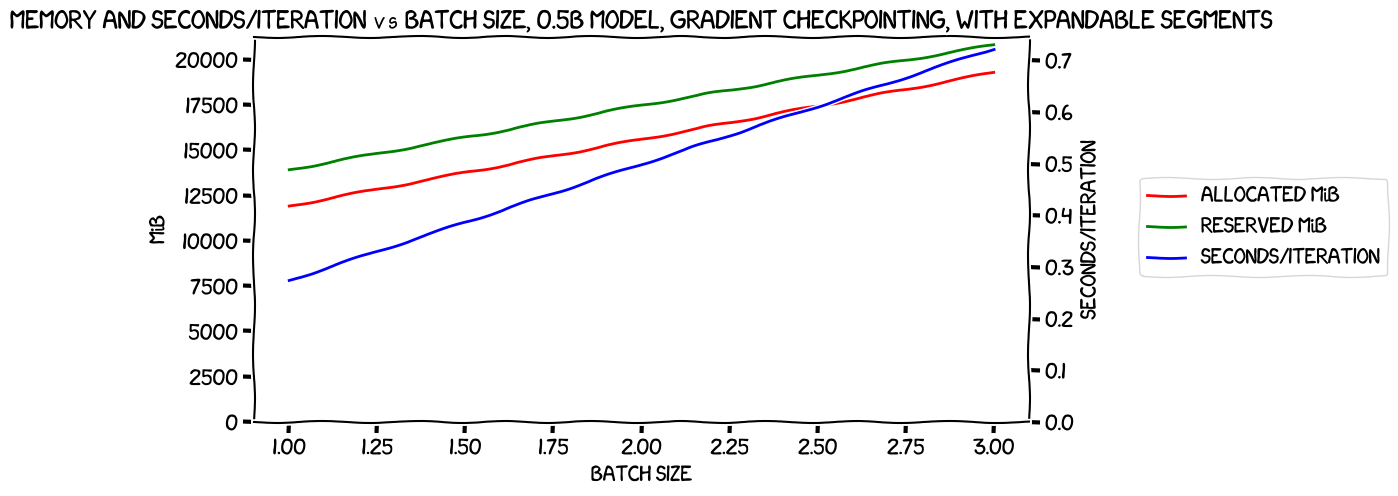
A very similar chart, and again a maximum batch size of three. Let's see how they compare; memory usage first:

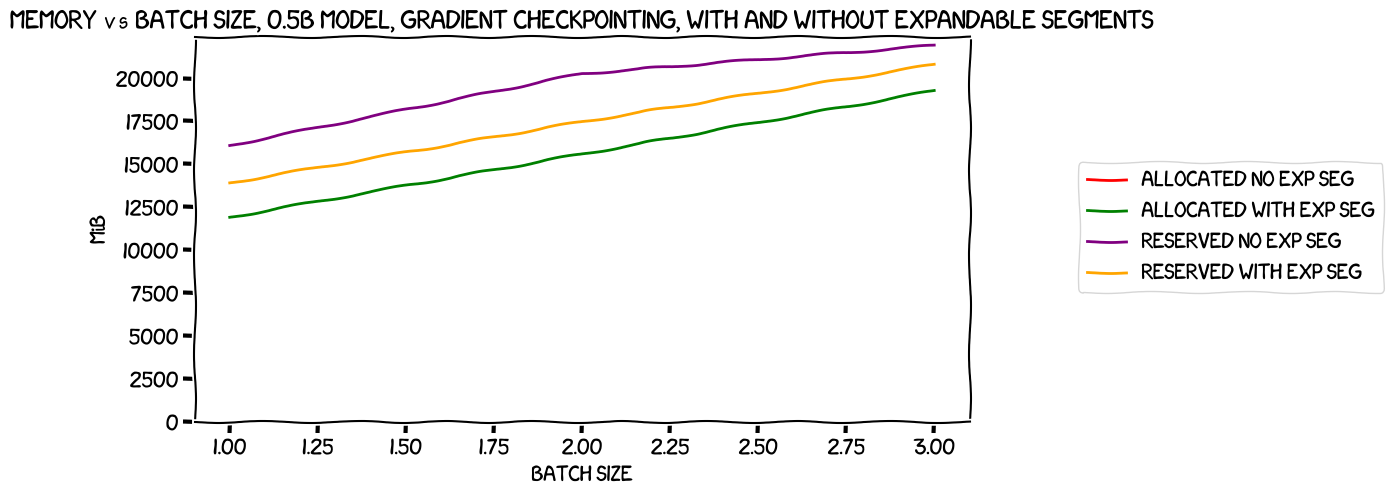
Memory usage vs batch size, 0.5B model, with gradient checkpointing, with and without expandable segments

There really are four lines on that chart, but as usual the allocated VRAM is the same with and without expandable segments -- after all, it's an improved memory allocation strategy that avoids "wasted" VRAM above and beyond what PyTorch needs -- the amount actually needed for the train is the same whether or not we use it, and that means that the allocated VRAM will generally be the same, at least in a small single-GPU train like this (it becomes more complex with multi-GPU, as I found a few posts back). Reserved VRAM, however, is -- as you'd expect -- lower with expandable segments (though not enough lower that we could fit in an extra batch).

Let's take a look at performance.

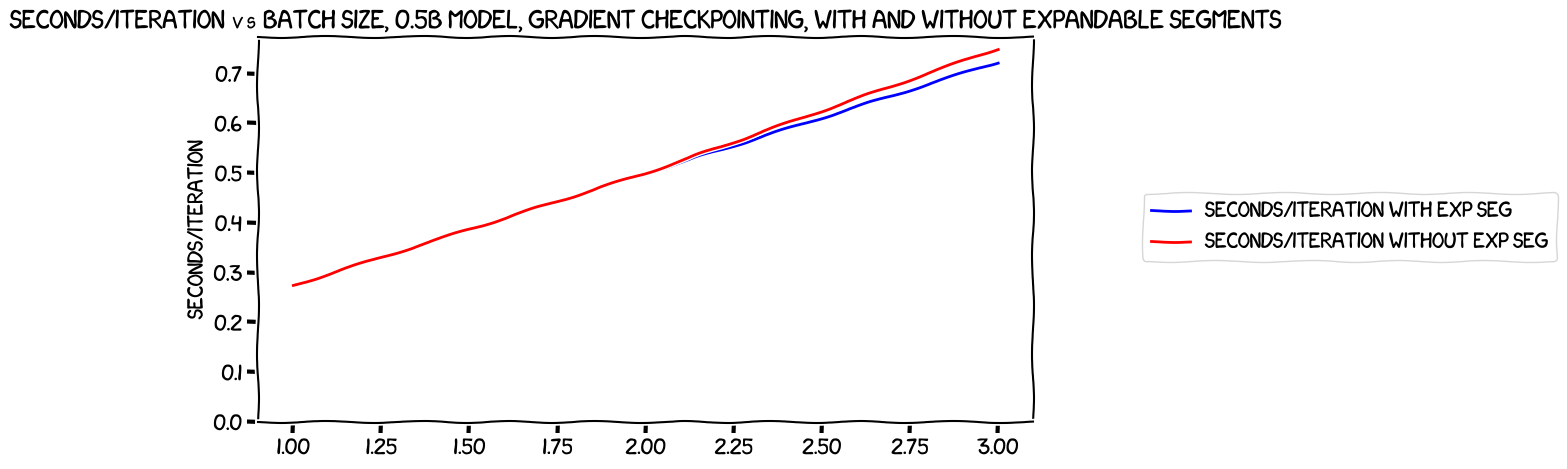
Seconds per iteration vs batch size, 0.5B model, with gradient checkpointing, with and without expandable segments

Note that this is using seconds/iteration, so lower is better. Pretty clearly, expandable segments has no real effect with a batch size of 1 or 2, but with three it helps a little bit and we're training very slightly faster when we use it. This matches up with the (to me a little counter-intuitive) result from before that expandable segments, despite being a slightly more complex memory management algorithm that saves memory, also speeds things up a bit. I think that might be because it's having to do somewhat less garbage collection, or some similar kind of operation -- if you look at the memory graph above, the reserved VRAM seems to be hitting the 23 GiB limit of the GPU's available VRAM at batch size three when not using expandable segments, which is perhaps adding on a memory management burden that just isn't there with expandable segments, as with that option the reserved VRAM is at around 20 GiB at the same batch size.

Anyway, having shown to my own satisfaction that using expandable segments was still a win, even with gradient checkpointing, it was time to see how these results matched up against the non-gradient-checkpointing ones. Here's a plot of the speed of the train both with and without checkpointing, both using expandable segments:

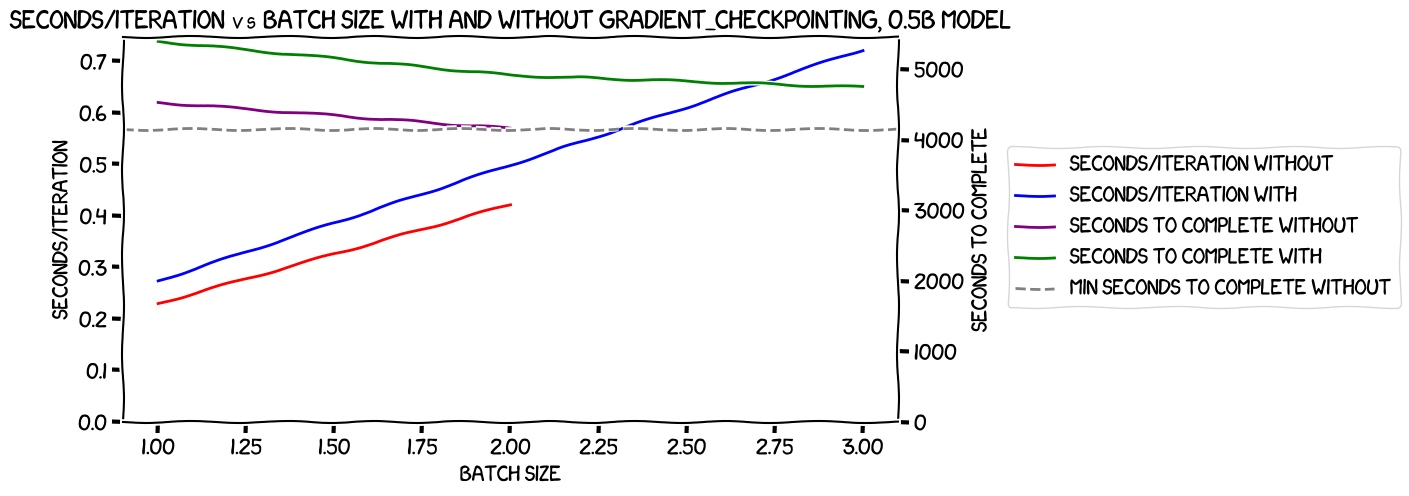
Seconds per iteration vs batch size, 0.5B model, with and without gradient checkpointing

There's a fair amount going on in that plot, so let's break it down:

This was a somewhat disappointing result for me, as I'd been hoping to see an immediate win, with gradient checkpointing allowing a batch size that would speed up training. However, it made a certain amount of sense; the activations for a 0.5B model, even at 16-bit, will be about a gig for a batch size of one, 2 GiB for 2, and so on. Looking at an allocated memory usage comparison (not reserved, as all we really care about here is the VRAM that is strictly necessary for the train in an imaginary world where there was no memory management overhead):

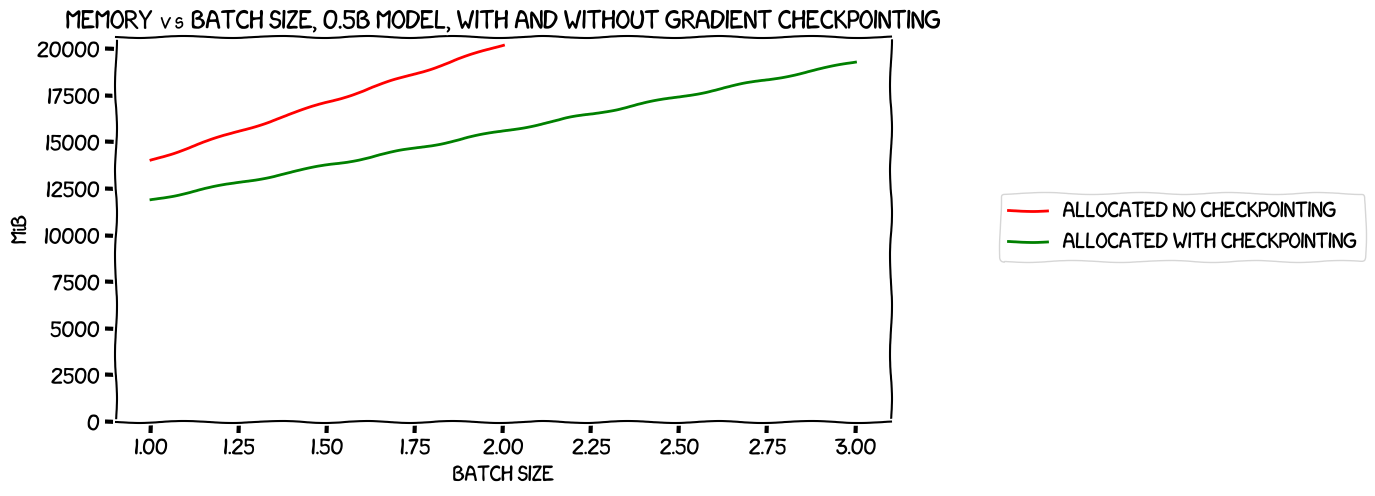
Memory vs batch size, 0.5B model, with and without gradient checkpointing

From that it looks a bit more like we're saving 2 GiB at a batch size of one, and four at batch size two. Perhaps the activations are being stored in 32-bit? Either way, it's pretty much in line with expectations.

Time to move on to the larger model.

Training the 8B model

As usual, for this I spun up an 8x A100 machine with 80 GiB VRAM on each GPU. The first time I did this I was hurrying through things and nervous about how much it was costing, but I've become kind of blase; better watch that so that I don't bankrupt myself...

The code change was, as before, just to add

model.gradient_checkpointing_enable()

...after creating the model, and again I initially ran it with and without expandable segments. One difference was immediately obvious; I was able to get a much larger batch size! Without gradient checkpointing, I had only been able to squeeze in a per-GPU batch size of 2, for an overall batch size of 16. But with gradient checkpointing, I could go all the way up to per-GPU 12, overall 96. That was pretty awesome. But would it help? We'd have to see. Here's the initial graph for the large model with gradient checkpointing, but without expandable segments:

Memory usage and seconds/iteration vs batch size, 8B model, gradient checkpointing, no expandable segments

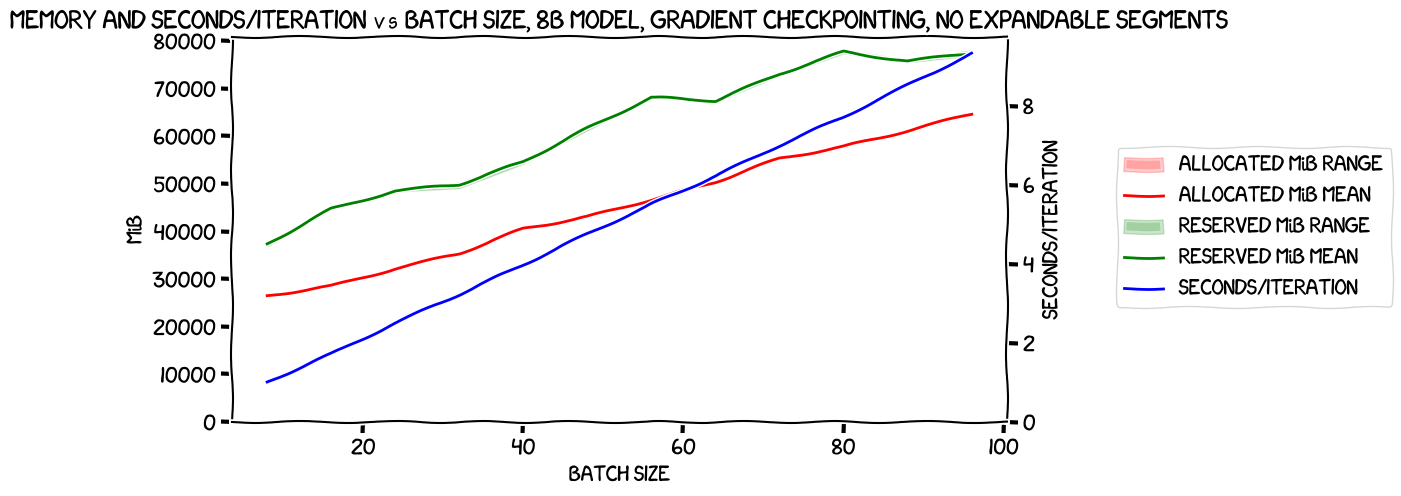
As with the last few tests, we're seeing a pretty tight range across GPUs of both the reserved and allocated memory. Reserved memory wibbles about a bit, but the trend is upwards; allocated memory goes up monotonically but not perfectly linearly. Seconds per iteration looks like a pretty much perfectly straight line.

Now, with expandable segments. This had one immediately obvious benefit: I was able to get the per-GPU batch size even higher, to 14 -- making an overall batch size of 112! Here's the chart:

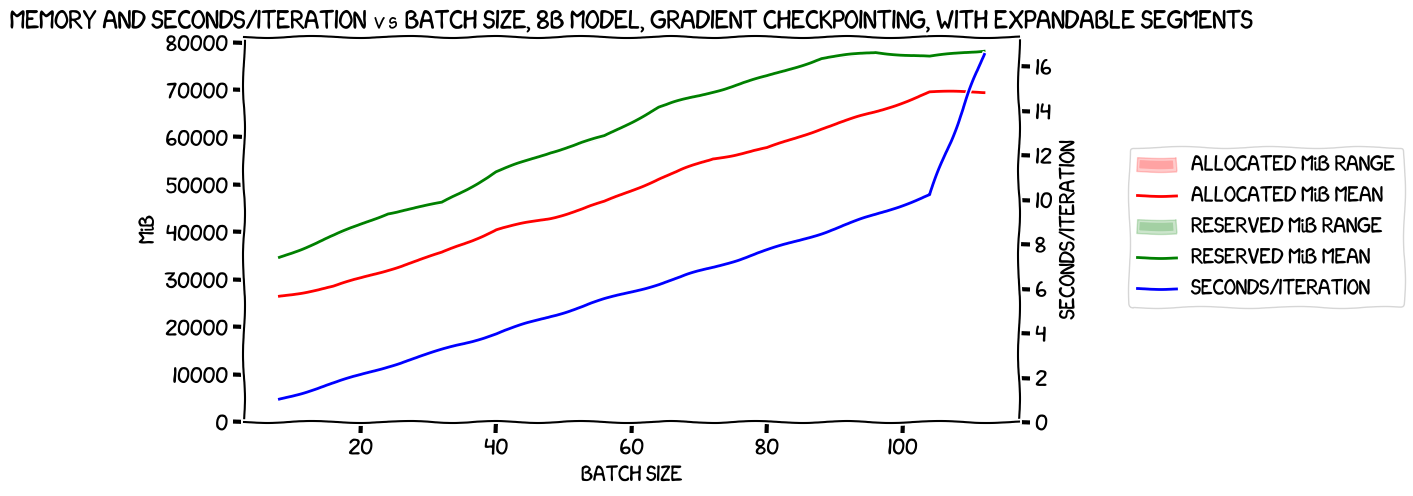
Memory usage and seconds/iteration vs batch size, 8B model, gradient checkpointing, with expandable segments

One thing stands out -- that last batch came in at a huge price in performance. Up to a batch size of 13/104, we have a nice linear increase in seconds/iteration, but then it spikes upwards. Looking at the allocated memory, it flattens out for that last iteration at 14/112 -- that is, allocated memory was the essentially the same as it was for the previous batch size. I'm going to handwave and say that PyTorch or some other level of the stack started throwing away caches to try to save memory there -- and strongly suspect that any gains we get in speed from larger batch sizes will cease at the batch size of 13/104 level.

But let's compare the two cases we have here, to see if once more, expandable segments costs nothing and gains something. Memory usage first:

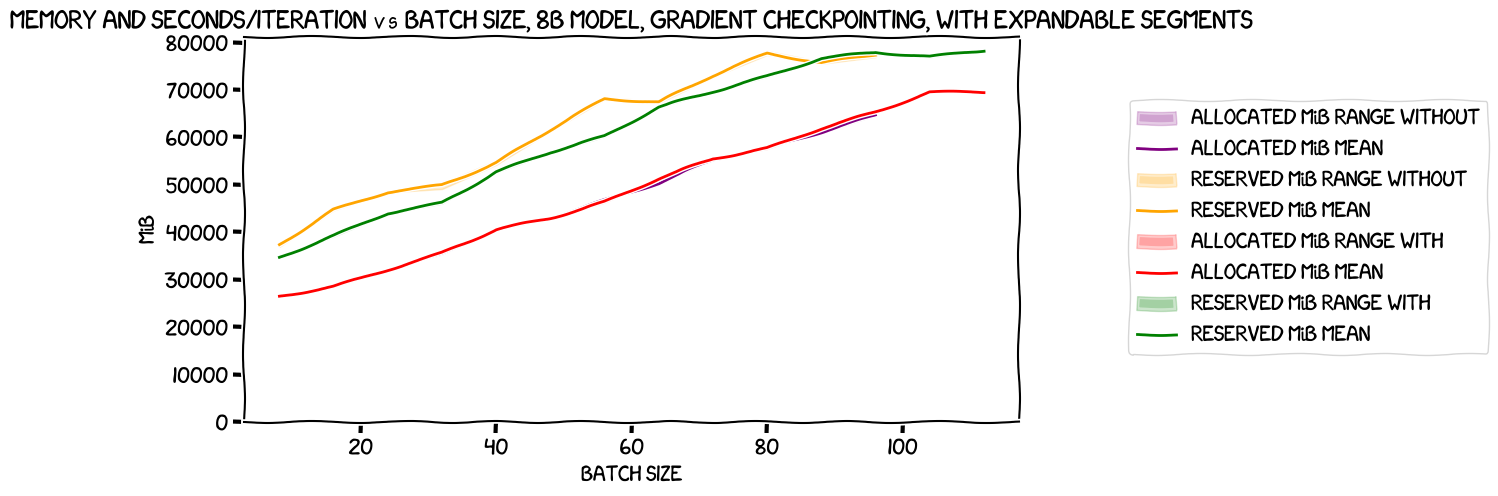
Memory usage vs batch size, 8B model, gradient checkpointing, with and without expandable segments

As expected, allocated memory both with and without expandable segments track each other almost perfectly (less perfectly than in the single-GPU case due to some kind of non-determinism caused by multi-GPU training, I think). Reserved memory savings from expandable segments are less obvious here -- indeed, there's a tiny bit at the end of the orange (reserved memory without expandable segments) that is a little bit lower than the green (reserved, with). Still, nothing amazingly surprising.

How about speed?

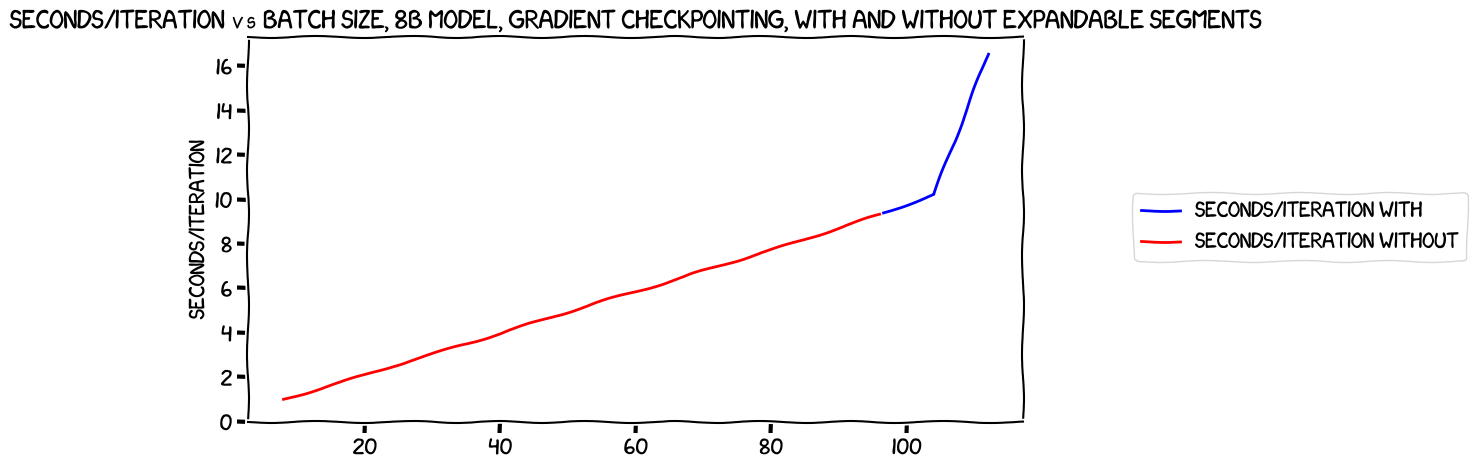
Seconds/iteration vs batch size, 8B model, gradient checkpointing, with and without expandable segments

They track each other perfectly -- so perfectly that I had to reverse the order in which the two lines were drawn in the graphing code so that you could see the red line for the run without expandable segments.

Once again, expandable segments brings a benefit -- a bump of one in the batch size we can use (strictly speaking, of two, but that performance hit for the last one makes it pretty obviously useless) -- and no cost.

So, throwing away the non-expandable-segments result, what do we see when we compare the speed with and without gradient checkpointing?

Seconds per iteration vs batch size, 8B model, with and without gradient checkpointing

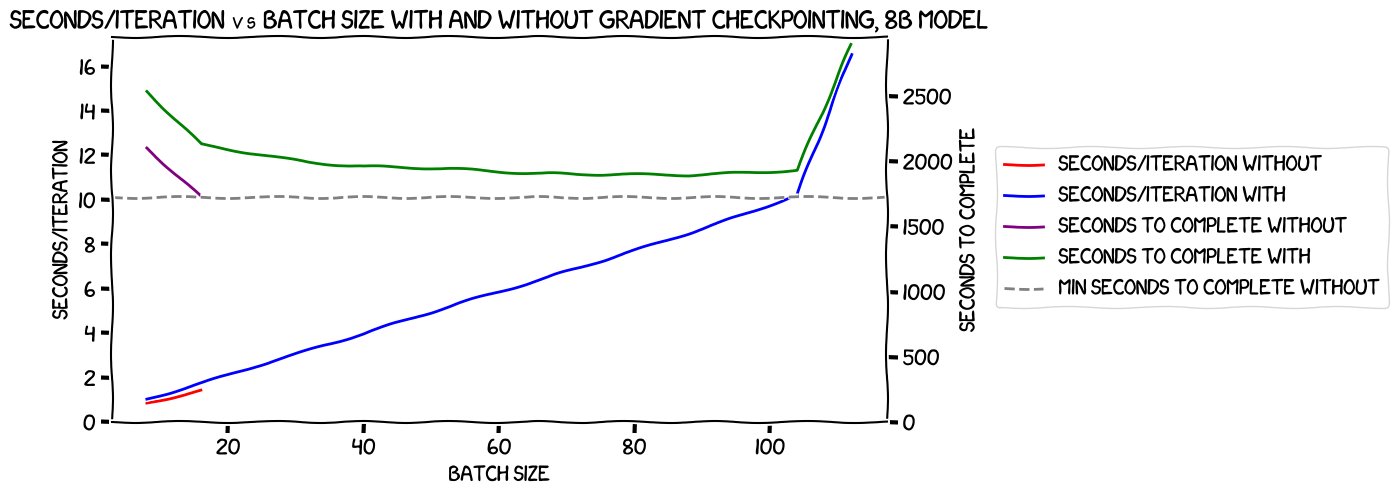
Well, damn. Even disregarding that last point with gradient checkpointing enabled (which, as predicted, massively increases time to complete), the green line showing the time to complete for the gradient checkpointing run never quite reaches the dotted line that is the time to complete for the non-checkpointing run with a batch size of 2 per GPU, 16 overall. The time to complete does go down over time -- it just never reaches that line. Boo.

Let's take a look at the memory usage, anyway:

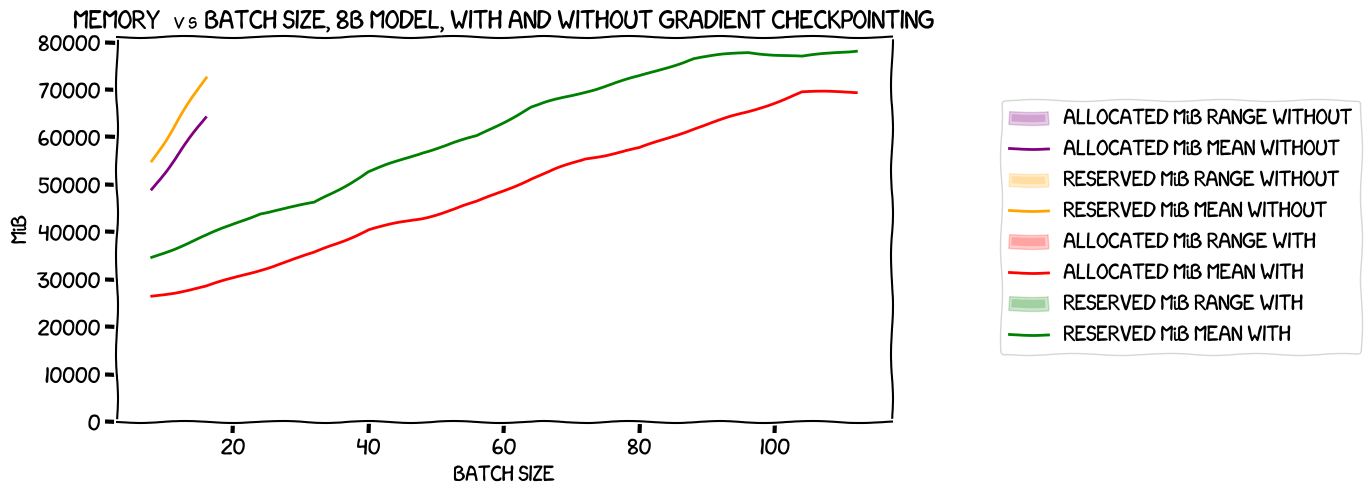
Memory vs batch size, 8B model, with and without gradient checkpointing

That actually is very interesting. Focusing on the purple line -- allocated memory without gradient checkpointing -- and the red one -- allocated memory with checkpointing -- there's about a 24GiB difference between the two at batch size one, and about 34 GiB at batch size two. We're working with an 8GiB model, and the activations for that should be either 16 GiB or 32 GiB per batch in the batch size (depending on whether they're 16-bit or 32-bit). Saving 24 GiB by gradient checkpointing makes sense if the activations are 32-bit (remember, we don't throw all of them away -- we keep those checkpointed ones). So let's say that that is what we're seeing.

But those numbers are per-GPU. I would expect the activations to be split across the different GPUs, so the 16-32GiB for the ones that are stored should only contribute 2-4GiB per GPU. Are they somehow duplicated across all GPUs? Given that the purpose of caching them is to speed things up during the backward pass, that might make sense; perhaps sending them from one GPU to another during that process is costly enough that it's not worth while from a caching viewpoint.

Conclusion

As a whole, this was a bit of a disappointment for me. From what I'd read, the cost of gradient checkpointing was, in general, cancelled out by the larger batch sizes it made possible. However, at least with my code, for this model and this training setup, with the hardware I had available, while it did allow larger batches, those larger batches did not make up for the performance loss.

Of course, it's perfectly possible that the larger batch sizes would be useful for other reasons -- like the better generalisation I mentioned earlier -- and of course gradient checkpointing could well be useful if you can't train at all without it.

And it's also well worth mentioning that this finding only holds for my code, with these models, this training setup and this hardware -- it's not something general. Perhaps there's something specific going on with my setup or these models; perhaps I'm somehow using more memory than I should (comparing my batch sizes to the ones in the examples on the Liger Kernels help pages suggests that I am), and if I fixed that, I could get the batch size high enough to overcome the checkpointing slowdown.

Or perhaps the problem is just that ZeRO needs to keep the activations -- or, at least, the checkpoints -- duplicated across all GPUs, so it's fundamentally more memory-hungry than other multi-GPU training systems like PipelineParallel (which, at least as I understand it, would be able to shard activations because, generally speaking, layers would be held in specific GPUs, and the activations would need to be "near" their layers for the backward pass).

There is (unsurprisingly) a lot more for me to learn here. But I think it's time to wrap this series up, and so I'll finish with a much-more strongly-held version of what I said at the end of the last post:

I think I'm finally in a place where I can do what should be the last experiment in this series: a full fine-tune of the Llama 3 8B base model -- on the openassistant-guanaco dataset, without using tricks like quantization or LoRA.

« Messing around with fine-tuning LLMs, part 8 -- detailed memory usage across batch sizes